图灵模式——Turing Pattern

我们之所以能够用科学来认知和解释这个宇宙中各种纷繁复杂的现象，一个重要前提就是这些复杂现象背后的规律是简单、有秩序的。如果规律比现象还复杂，那么人类将永远不能认识它。在这个意义上，我相信，一切复杂都来源于简单的叠加。
——遥远地方剑星

21世纪的社会，大众都知道通过指纹、虹膜等生物特征可以识别每个人，这是因为每个人的指纹、虹膜都是独一无二的。其实不止是人类，很多动物的花纹、图案等也都可以用来识别个体，比如每只老虎、每匹斑马、每头金钱豹的花纹也都是唯一的。2007年陕西农民周正龙声称拍到了野生华南虎，后来被发现是照着一张更早的年画上的华南虎拍摄的（图1）。之所以能确认这一点，正是依据年画上的华南虎和周正龙拍摄的华南虎的斑纹是相同的这个理由，著名华人神探李昌钰也是通过这一点确信周正龙在造假。为什么动物和人身上都会有这种看起来整体类似、而细节上每个个体又完全不同的斑纹或纹理呢？1952年，英国伟大的科学家图灵最早研究了这个问题。

阿兰·图灵（Alan Mathison Turing，1912年6月23日~1954年6月7日）是我非常钦佩的一位科学家，他因同性恋这个特殊的原因不能见容于时代而自杀，实在是科学上的重大损失和人类历史上的巨大悲剧。图灵生于乱世，青春年华之时正赶上第二次世界大战，他依靠他卓越的天赋通过破译德军的通讯密码而为同盟国的胜利做出了贡献。他更主要的贡献是在科学上，我们今天熟知的图灵测试、图灵机都来源于图灵。如今计算机领域的最高奖项图灵奖也是以他的名字命名。图灵是20世纪伟大的计算机科学家、数学家、逻辑学家、密码分析学家、理论生物学家 ，被公认为“计算机科学之父”、“人工智能之父” 。

我们今天就来介绍一下图灵在理论生物学领域的一个重大成果——图灵模式（Turing Pattern），这个成果阐明了生物体为什么会形成整体上类似、个体间又互不相同的斑纹，它告诉我们这个复杂现象的背后有着一个简单、直接的原因。可能有的朋友奇怪，图灵作为一个数学家、计算机科学家，为什么在生物科学领域做出了贡献呢？其实在我看来，图灵的这个成果仍然属于数学领域，只不过图灵利用他那天才的头脑把数学分析应用到了生物和化学领域，对一种现象做出了解释。这也从另一个角度说明了数学在人类生产生活中发挥的巨大作用。事实上，囿于当时生物科学发展水平，图灵在生物学上的一些观点并不都正确，但是图灵在数学上对这一现象做出的解释则是正确的，图灵模式理论到今天仍然指导着生物学、化学等领域在这一方向上的研究。

本文对图灵模式的介绍完全基于图灵1952年的论文《The Chemical Basis of Morphogenesis》（中文名《形态发生的化学基础》），希望感兴趣的朋友能从中了解图灵伟大的思想。我本人在读完了这篇论文后对图灵高超的数学计算能力深感佩服以至于崇拜，似乎图灵有着一双能直接看穿复杂偏微分方程数学计算的透视眼。

一、图灵认为生物体能够产生“形态”的原因

图灵认为生物体是由细胞构成的，之所以生物体能够形成不同的“形态”，是因为组成生物体的细胞中使其产生“形态”的物质（图灵称之为形态发生素，morphogens）浓度不同。这种观点用来解释斑纹是很容易理解的，比如老虎身上黑黄相间的条纹是由于构成黑色和黄色部分的机体的细胞中相应物质（形态发生素）的浓度不同。图灵的论文重点研究的就是这些不同种类的物质（形态发生素）的浓度是如何变化的。

图灵的论文中还阐述了多种物质发生化学反应时对稳定性破坏的可能、有机体的对称性（如旋转对称、镜像对称等）对这些反应的影响等，这里面很多的观点都不是很准确甚至不正确了，但是图灵认为这些“形态发生素”浓度的变化是由于它们在细胞间的扩散和细胞内部发生的化学反应所决定的这个观点还是可靠的。

既然是这样，那么下面图灵重点研究的就是“化学反应”与“物质扩散”综合作用的详细过程了，这个过程今天在数学上用被称为“反应扩散方程”（Reaction-diffusion Equation）的偏微分方程组来描述。

二、图灵研究的反应扩散方程

对微分方程了解少的朋友可能想不到，微分方程是一种典型的从简单结构产生复杂结果的数学工具，尤其是偏微分方程组。著名的“蝴蝶效应”产生的原因就是由于气象预报需要数值求解一组偏微分方程，美国气象学家爱德华·洛伦兹（Edward N.Lorenz）最早发现这些偏微分方程组的解对初始值高度敏感，从而打了“蝴蝶效应”这样一个比方，使人们对于数学上的混沌现象有了形象化的理解。

图灵在研究生物形态产生的过程中也遇到了求解偏微分方程组的问题，当然，图灵的数学能力肯定要高于气象学家爱德华·洛伦兹，虽然偏微分方程组高度复杂，但是图灵仍然从中发现了一些有价值的规律。

1.求解细胞环上的反应扩散微分方程组

图灵论文《The Chemical Basis of Morphogenesis》的核心工作是研究了由 N 个细胞构成的细胞环上的“反应-扩散”过程，如图2所示。我们知道，“环”是一维空间结构，扩散过程发生在一维空间结构上总比发生在二维、三维空间上要简单些，图灵重点研究了这种最简单的情况。但后面我们会看到，其实这种最简单的情况对应的数学求解过程也很复杂，其解的形态就更是复杂无比了。图灵能够从极为复杂的求解过程中发现规律，充分展现了他那无与伦比的数学天才。

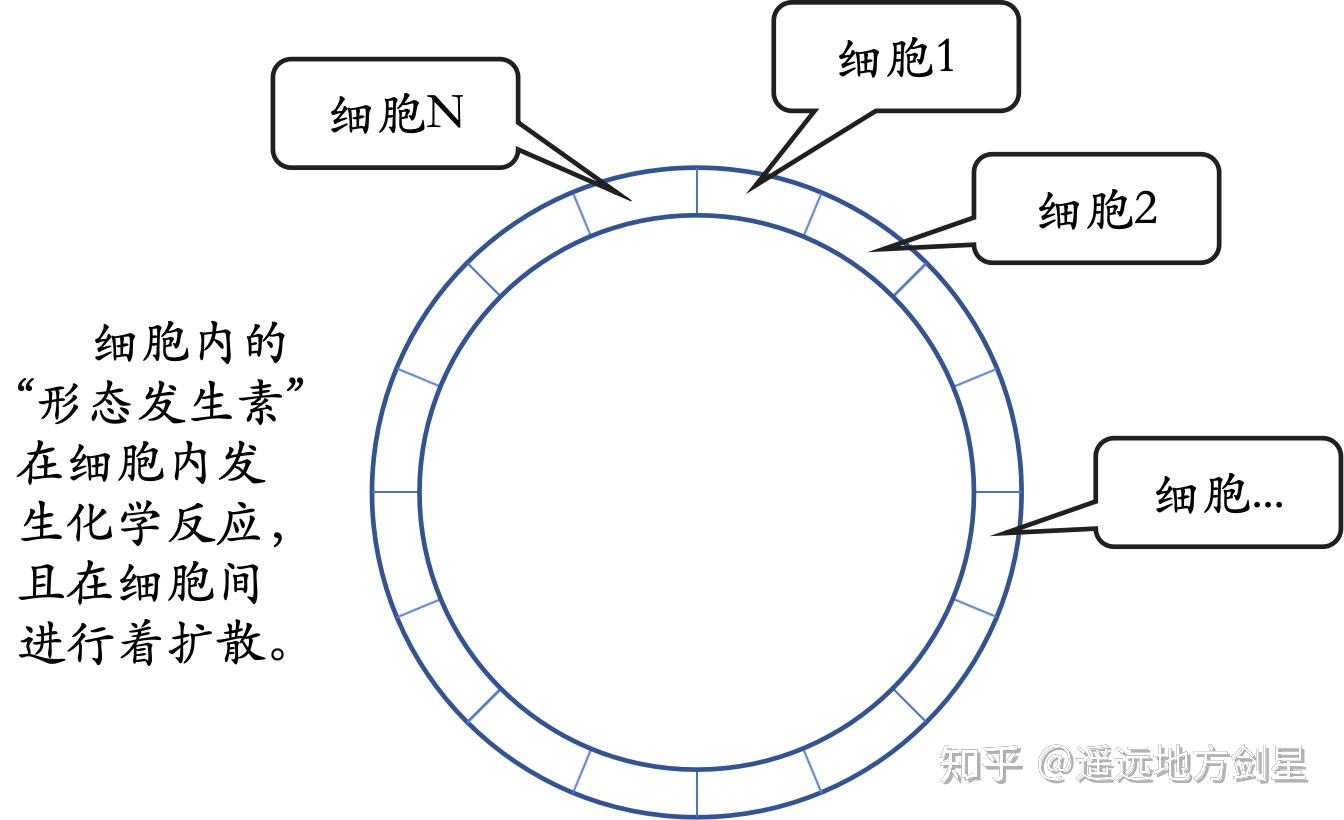
图灵认为，细胞内的“形态发生素”发生着多种复杂的化学反应，图灵仍然从最简单的情况入手，先假定只有两种“形态发生素”，图灵在论文中指出，读者可以将两种“形态发生素”扩展到任意数量，但是“形态发生素”超过3个时，在本质上没有新的特性出现。

上面的内容其实就是图灵对于生物体“形态生成”所建立的简易模型，然后图灵将其数学化。设两种“形态发生素”分别为 X 和 Y ，其在第 i 个细胞中的浓度分别为 ${𝑋}_{𝑖}$ 和 ${𝑌}_{𝑖}$ ；X 、Y 的浓度随时间的变化率一方面与 X 、Y 之间的复杂化学反应过程有关（参与反应的物质未必只有 X 和 Y，还可能有其他物质，这些物质可能起到催化作用，也可能参与反应但物质本身与形态发生无关），另一方面也与 X 、Y 沿着细胞环扩散有关，也就是说浓度变化率是化学反应与物质扩散两个因素的叠加。从而，图灵给出了下面的微分方程，

$\begin{array}{l}\frac{𝑑{𝑋}_{𝑟}}{𝑑𝑡}=𝑓({𝑋}_{𝑟},{𝑌}_{𝑟})+𝜇\cdot ({𝑋}_{𝑟+1}-2{𝑋}_{𝑟}+{𝑋}_{𝑟-1})\\ \frac{𝑑{𝑌}_{𝑟}}{𝑑𝑡}=𝑔({𝑋}_{𝑟},{𝑌}_{𝑟})+𝜈\cdot ({𝑌}_{𝑟+1}-2{𝑌}_{𝑟}+{𝑌}_{𝑟-1})\end{array}𝑟=(1,2,...,𝑁)...(1)<span\; style="font-family:-apple-system,\; BlinkMacSystemFont,\; "Helvetica\; Neue",\; "PingFang\; SC",\; "Microsoft\; YaHei",\; "Source\; Han\; Sans\; SC",\; "Noto\; Sans\; CJK\; SC",\; "WenQuanYi\; Micro\; Hei",\; sans-serif;font-size:medium;">式（1）中函数\; f\; 和\; g\; 表示由化学反应导致的两种“形态发生素”的变化率， </span>$

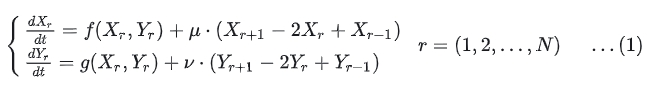
$𝜇、𝜈$ 分别表示两种物质在细胞间的扩散系数。根据一般扩散理论，扩散速度与扩散系数及浓度的二阶差分（对于连续函数就是 $\mathrm{\Delta }𝑋、\mathrm{\Delta }𝑌$ ， $\mathrm{\Delta }$ 为拉普拉斯算子）成正比。由于细胞组成了环状，所以我们将 ${𝑋}_0$ 与 ${𝑋}_{𝑁}$ 、 ${𝑋}_{𝑁+1}$ 与 ${𝑋}_1$ 视为相同。

在式（1）的微分方程所表达的规律的作用下，“形态发生素” X 和 Y 会达到某种平衡，从而形成了稳定的 X、Y 的状态。图灵之所以确认这一点，是因为无法平衡的反应扩散过程是无法在真实的生物体中存在的。

下面则是图灵研究的最关键内容了：图灵认为在平衡态达成后，由于扰动，“形态发生素” X 和 Y 的浓度都会发生微小的变化，这种变化会导致扰动以另一种反应扩散的方式传播开来，这种扰动导致的变化不见得都能很快回到平衡态，有时会形成新的状态。

既然是扰动，我们可以假定“形态发生素”的浓度由原来平衡时的 X 和 Y 变成了 X+x 和 Y+y ，而且 x 和 y 在数值上都是小量，从而
$$\begin{gathered} 𝑓({𝑋}_{𝑟},{𝑌}_{𝑟})\approx 𝑓(𝑋,𝑌)+𝑎\cdot 𝑥+𝑏\cdot 𝑦 \\ 𝑔({𝑋}_{𝑟},{𝑌}_{𝑟})\approx 𝑔(𝑋,𝑌)+𝑐\cdot 𝑥+𝑑\cdot 𝑦 \end{gathered}$$
显然在上式中我们取了一阶近似，a、b、c、d都是相应的系数。

由此，微分方程（1）变为下面新的方程（2），

$\{\begin{array}{l}\frac{𝑑{𝑥}_{𝑟}}{𝑑𝑡}=𝑎\cdot {𝑥}_{𝑟}+𝑏\cdot {𝑦}_{𝑟}+𝜇\cdot ({𝑥}_{𝑟+1}-2{𝑥}_{𝑟}+{𝑥}_{𝑟-1})\\ \frac{𝑑{𝑦}_{𝑟}}{𝑑𝑡}=𝑐\cdot {𝑥}_{𝑟}+𝑑\cdot {𝑦}_{𝑟}+𝜈\cdot ({𝑦}_{𝑟+1}-2{𝑦}_{𝑟}+{𝑦}_{𝑟-1})\end{array}𝑟=(1,2,...,𝑁)...(2)$

下面，图灵将用一种巧妙的方法求解式（2）这 2N 个微分方程构成的微分方程组，对于数学计算推导不感兴趣的朋友可以略过这部分内容。

以上就是图灵求得的细胞环上的反应扩散方程的解。当然，如果式（7）关于 p 的方程有重根，那么解的形式会有变化，图灵也进行了分析，我们就不说那么细了，毕竟在实际的反应扩散过程中，重根是一种特定的、甚至是理想的情况。

同步图灵也研究了把上述离散化的微分方程组变为连续化的偏微分方程组，并指出离散状态和连续状态并没有带来本质的不同。所以，后面我们就都基于上面离散化的方程的解来继续介绍了，而且这也有利于我们进行数值计算。

图灵继续指出，式（8）这个微分方程的解本身过于复杂，不能提供有价值的信息，但是这难不倒图灵这样的大师，他继续给出了这个解基于时间渐进行为的分析。

2.细胞环反应扩散过程的时间渐进行为分析

虽然式（8）给出的解是一个很复杂的形式，但是图灵敏锐地指出，随着时间 t 的增加，那些具有最大实部的 ${𝑝}_{𝑠}$ 和 ${𝑝}_{𝑠}^{\prime }$ 项将成为主导项，其它项则可以忽略。另外，图灵还分析发现主导项未必只有一个，因为很容易得到 ${𝑝}_{𝑠}={𝑝}_{𝑁-𝑠}$ ，且 $𝑅𝑒({𝑝}_{𝑠})=𝑅𝑒({𝑝}_{𝑠}^{\prime })$ ，这两种情况决定了主导项可能比较多。因此，对于一般人来说，分析清楚主导项已经不容易了，可是图灵在论文中信手拈来，直接给出了总共的六种情况（a、b、c、d、e、f），并且证明了每种情况都是可能实际发生的。

图灵给出的这六种情况中，有两种情况（“情况 e” 和“情况 f”）是需要三种或以上的“形态发生素”才可能存在的，另外四种情况中有一种“情况d”是图灵认为“最令人感兴趣的，具有最普遍的生物应用”（“This is the case which is of greatest interest, and has most biological application.”），我在这篇文章中介绍包括这种“最令人感兴趣”的“情况d”在内的两种情况，并给出计算机的模拟。

2.1 图灵论文中的情况（a）—— 极长波长静止情况

图灵指出：当取 $𝜇=𝜈=\frac{1}{4}$ 、 $𝑏=𝑐=1$ 、 $𝑎=𝑑$ 时，带入方程（7），很容易发现 ${𝑝}_{𝑠}=𝑎-𝑠𝑖{𝑛}^2\frac{𝜋𝑠}{𝑁}+1$ 是实数，且在 $𝑠=0$ 时取到最大值。这是比较特殊的情况，因为此时主导项只有一项，此时每个细胞中的干扰都会被同步的放大，从而脱离平衡态。

在图灵的时代，电子计算机刚刚诞生，都是电子管计算机，用今天的眼光看来，属于性能很差、耗电很大、成本高昂的东西。所以图灵在1952年写这篇论文的时候，是没有可能给出很充分的计算机模拟的。单凭数学推导和手工计算，就能发现这样复杂的规律，图灵实在是了不起。

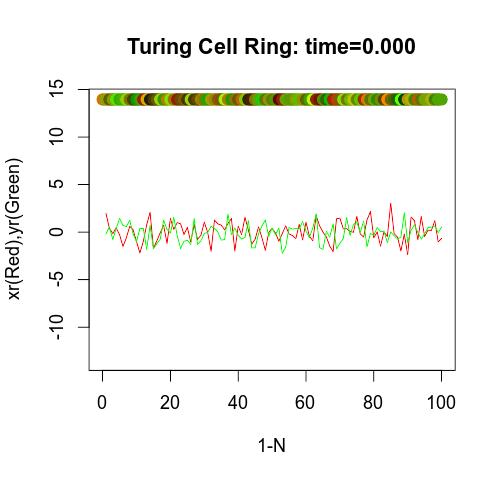
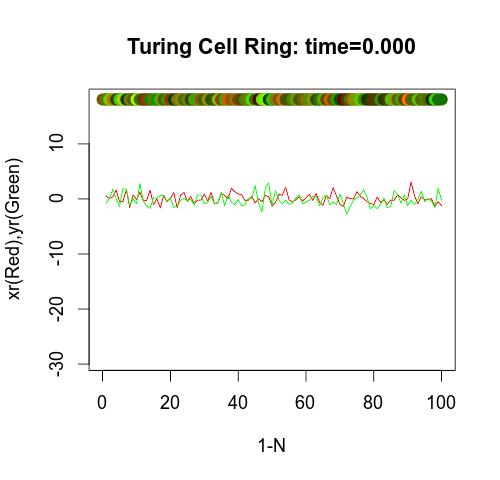
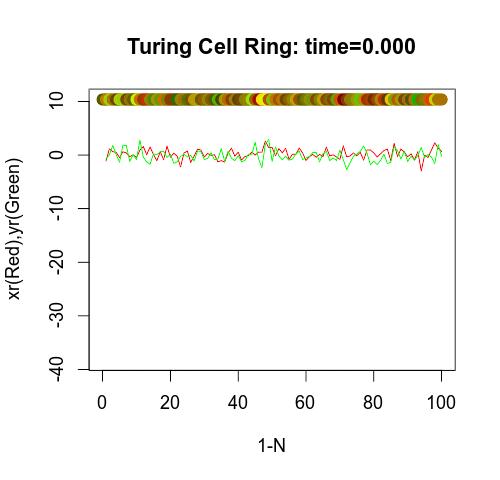
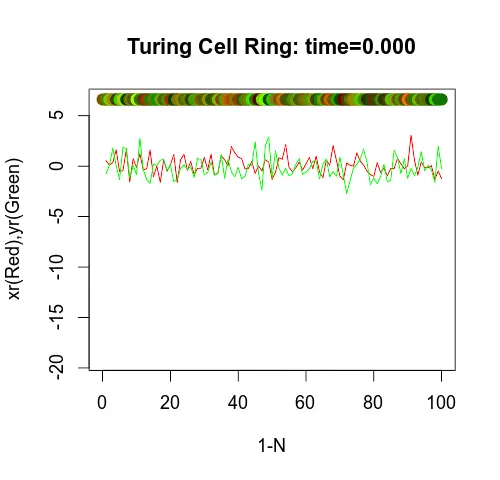
今天的我们已经可以很容易的对图灵的结论进行计算机模拟验证了。下面的动图3是我对“情况a”的模拟。

从图3中可以看出，“形态发生素”X和Y的浓度受到干扰后（我设置的初始干扰是均值为0、方差为1的正态分布），不但没有恢复到平衡位置（相当于0点），反而将干扰同步放大，而且是真正的同步放大，各个细胞间步调完全一致。如果X表征红色、Y表征绿色，那么这个细胞环就会形成类似图3中上面的色带的纹理。

这种情况并不是一种有趣的情形，因为干扰造成的纹理必然是杂乱无章的，同步放大之后也仍然还是杂乱无章的。生物体的斑纹肯定不是在这种条件下形成的。

2.2 图灵论文中的情况（d）—— 有限波长的驻波

“情况d”才是图灵认为最有趣的情形。我这篇文章会着重分析这种情况，不仅分析图灵论文中的一维情况（细胞环），而且还会模拟下二维的情况，让大家看到真正的图灵斑纹。

图灵指出：当取 $𝑎=𝐼-2$ 、 $𝑏=2.5$ 、 $𝑐=-1.25$ 、 $𝑑=𝐼+1.5$ 、 $𝜇=2\cdot 𝜈$ 时，带入方程（7）会得到 $(𝑝-𝐼{)}^2+(\frac{1}{2}+6\cdot 𝜇𝑠𝑖{𝑛}^2\frac{𝜋𝑠}{𝑁})(𝑝-𝐼)+\frac{1}{2}(4\cdot 𝜇𝑠𝑖{𝑛}^2\frac{𝜋𝑠}{𝑁}-\frac{1}{2}{)}^2=0$ 。此时，如果存在合适的整数 ${𝑠}_0$ 使得 $𝜇𝑠𝑖{𝑛}^2\frac{𝜋{𝑠}_0}{𝑁}=\frac{1}{8}$ ，即常数项为 0 ，则 $𝑝=𝐼$ 成为实部最大的主导项，细胞环上将存在着 ${𝑠}_0$ 个波峰；如果不存在这样的整数 ${𝑠}_0$ ，那么波峰数将是使 $𝜇𝑠𝑖{𝑛}^2\frac{𝜋{𝑠}_0}{𝑁}$ 最接近 $\frac{1}{8}$ 的整数 ${𝑠}_0$ (个别情形下会相差正负 1)。

下面我们具体模拟几个例子：

（1）取 $𝐼=3,𝜇=10,𝜈=5,𝑁=100$ ，此时计算使 $𝜇𝑠𝑖{𝑛}^2\frac{𝜋{𝑠}_0}{𝑁}$ 等于 $\frac{1}{8}$ 的 ${𝑠}_0\approx 3.56$ ，按照图灵的判断应该形成3～4个波峰。图4-1 是模拟得到的结果。

图4-2 是在不改变参数，仅仅将 X 的初始干扰值重新取了一组随机数后得到的结果，可以看到，波峰仍然是3个，但是形态已经与图4-1 有所不同了。这就是为什么同类生物斑纹总体类似、个体却互不相同的原因。

（2）取 $𝐼=3,𝜇=40,𝜈=20,𝑁=100$ ，此时计算使 $𝜇𝑠𝑖{𝑛}^2\frac{𝜋{𝑠}_0}{𝑁}$ 等于 $\frac{1}{8}$ 的 ${𝑠}_0\approx 1.78$ ，按照图灵的判断应该形成1～2个波峰。图5 是模拟得到的结果。

从图5的色带中可以看出，波峰数少了之后，斑纹也变成了两段黑色纹理。

如果对微分方程比较熟悉的朋友可能会想到，按照图灵的解方程和分析方法，如果把式（2）一维的反应扩散方程变为二维，那么其分析结果是类似的。图灵在论文中也指出了这一点。变为二维条件后，设两个维度分别为 ${𝑟}_1、{𝑟}_2$ ，即

$\{\begin{array}{l}𝑥={𝑥}_{{𝑟}_1,{𝑟}_2}=𝑥({𝑟}_1,{𝑟}_2,𝑡)\\ 𝑦={𝑦}_{{𝑟}_1,{𝑟}_2}=𝑦({𝑟}_1,{𝑟}_2,𝑡)\end{array}{𝑟}_1=(1,2,...,𝑁),{𝑟}_2=(1,2,...,𝑁)$

式（2）的反应扩散方程变为

$\{\begin{array}{l}\frac{\mathrm{\partial }𝑥}{\mathrm{\partial }𝑡}=𝑎\cdot 𝑥+𝑏\cdot 𝑦+𝜇\cdot ({𝑥}_{{𝑟}_1-1,{𝑟}_2}+{𝑥}_{{𝑟}_1+1,{𝑟}_2}-2{𝑥}_{{𝑟}_1,{𝑟}_2}+{𝑥}_{{𝑟}_1,{𝑟}_2-1}+{𝑥}_{{𝑟}_1,{𝑟}_2+1}-2{𝑥}_{{𝑟}_1,{𝑟}_2})\\ \frac{\mathrm{\partial }𝑦}{\mathrm{\partial }𝑡}=𝑐\cdot 𝑥+𝑑\cdot 𝑦+𝜈\cdot ({𝑦}_{{𝑟}_1-1,{𝑟}_2}+{𝑦}_{{𝑟}_1+1,{𝑟}_2}-2{𝑦}_{{𝑟}_1,{𝑟}_2}+{𝑦}_{{𝑟}_1,{𝑟}_2-1}+{𝑦}_{{𝑟}_1,{𝑟}_2+1}-2{𝑦}_{{𝑟}_1,{𝑟}_2})\end{array}...(9)$

很容易看出式（8）的通解只需要修改为下面的式（10）就满足方程（9）了，因为式（10）中的两个维度的坐标 ${𝑟}_1、{𝑟}_2$ 完全不耦合。

$\{\begin{array}{l}{𝑥}_{𝑟}=\sum _{𝑠=0}^{𝑁-1}({𝐴}_{𝑠}{𝑒}^{{𝑝}_{𝑠}𝑡}+{𝐵}_{𝑠}{𝑒}^{{𝑝}_{𝑠}^{\prime }𝑡})\cdot (𝑒𝑥𝑝[\frac{2𝜋𝑖{𝑟}_1𝑠}{𝑁}]+𝑒𝑥𝑝[\frac{2𝜋𝑖{𝑟}_2𝑠}{𝑁}])\\ {𝑦}_{𝑟}=\sum _{𝑠=0}^{𝑁-1}({𝐶}_{𝑠}{𝑒}^{{𝑝}_{𝑠}𝑡}+{𝐷}_{𝑠}{𝑒}^{{𝑝}_{𝑠}^{\prime }𝑡})\cdot (𝑒𝑥𝑝[\frac{2𝜋𝑖{𝑟}_1𝑠}{𝑁}]+𝑒𝑥𝑝[\frac{2𝜋𝑖{𝑟}_2𝑠}{𝑁}])\end{array}...(10)$

当然，图灵那个时代计算一维的数据已经非常不容易了，图灵不太可能完成二维数据的模拟计算(虽然难，但图灵在论文中仍给出了一个大致的二维斑纹图形示例)。今天的我们当然可以做到这一点。

（3）二维条件下，我们选取与（1）中类似的参数， $𝐼=3,𝜇=100,𝜈=50,{𝑁}_{{𝑟}_1}={𝑁}_{{𝑟}_2}=150$ ，此时计算使 $𝜇𝑠𝑖{𝑛}^2\frac{𝜋{𝑠}_0}{𝑁}$ 等于 $\frac{1}{8}$ 的 ${𝑠}_0\approx 1.69$ ，按照图灵的判断应该在 ${𝑟}_1$ 和 ${𝑟}_2$ 每个单一维度上都能够形成1～2个波峰。但是，二维情况下叠加后的图像则要更加复杂，总体上的斑点数量要显得更多。图6-1 、6-2是在同样参数、只是初始随机扰动不同的情况下模拟得到的结果。

到这里，更为形象的图灵斑纹终于现身了。完全一样的参数，仅仅是初始扰动不同，就产生了类似但细节不同的斑纹，图灵的论文告诉我们，生物体上的斑纹就是这样一个原理。人类的指纹、虹膜，老虎、豹子的条纹和斑点可以用于个体识别的根本原因也在这里。

（4）如果我们选取 $𝜇$ 更大一些的参数， $𝐼=3,𝜇=200,𝜈=100,{𝑁}_{{𝑟}_1}={𝑁}_{{𝑟}_2}=150$ ，此时计算使 $𝜇𝑠𝑖{𝑛}^2\frac{𝜋{𝑠}_0}{𝑁}$ 等于 $\frac{1}{8}$ 的 ${𝑠}_0\approx 1.19$ ，模拟得到的斑点数量应该会更少一些，如图7所示。

三、总结与思考

图灵对生物体斑纹形成的解释是具有指导意义的。他第一次创造性的通过反应扩散过程解释了生物体形成斑纹或者斑点的原因，并且运用自己高超的数学技巧和计算能力，在大规模数值计算尚不具备条件的上世纪50年代，精准的阐释了“微分方程”+“随机干扰”造成的斑纹形成的理论。因此，今天我们还将很多生物体斑纹、化学反应形成的某种模式甚至是震荡模式统称之为图灵模式（Turing Pattern）。

图灵模式的理论告诉我们，生物体复杂斑纹的形成是有着简单直接的原因的，那就是多种物质发生化学反应的同时还发生着物理扩散现象，这是一个经典的物理化学过程。正如我这个系列文章的标题，一切复杂都来源于简单的叠加。

稍微多思考下，如果扩散过程不是各向同性的（比如在某些晶体或者具有晶体特性的环境内），那么形成的图灵模式就很可能不是斑点而是条纹；如果图灵所说的“形态发生素”对形态的形成也不是线性的关系，那么最终构成的形态就会更加复杂多样。

本文最后一个例子就是设定了形态发生素 X 和 Y 沿着两个不同方向扩散的速度相差100倍，而且对构成颜色的作用也是非线性的（相当于是一个颜色滤波器），那么就会形成类似老虎身上的条纹样图案，如图8 。